5. Függvények

Ezen az órán a függvényekkel, a rekurzióval és a debuggolással ismerkedtünk meg. Az órán írt kódok kommentekkel kiegészítve (és a 4. házi megoldása) a szokásos GitHub repository-ban érhető el:

https://github.com/Dawars/Trefort-Android-Szakkor/blob/master/src/Szakkor5Ora.java

Függvények

Ha egy kódrészletet többször szeretnénk használni, akkor érdemes függvényt használni. így a kód csak egy helyen fordul elő, könnyebb módosítani és átláthatóbb.

Vegyük a következő példát: Javaban nincsen külön művelet a hatványozásra, de mi sokszor szeretnénk ezt használni.

Először írjunk egy kódrészletet, ami kiszámolja a $latex base^n $ eredményét.

A hatványozás az a művelet, ahol a base -t n -szer összeszorozzuk. Pl: \(2^3 = 2 * 2 * 2 = 8\)

double base = 2;
int n = 3;

//—————————-

double result = 1; // eredmény
for(int i = 0; i < n; i++)
    result = result * base;

//—————————-

System.out.println(result); // Kiírja, hogy 8

(Remélem) látjuk, hogy ezt felesleges és fárasztó lenne minden alkalommal kiírni.

Most ezt alakítsuk át egy egyszerű függvénnyé:

// a static kulcsszóról következő órán beszélünk, csak ezért raktam zárójelbe
  
/**
* Hatványozó függvény
*
* double base - hatványalap
* double n - hatványkitevő, hányszor szorozzuk össze a base-t
* @return base ^ n
*/
(static) double hatvanyozas(double base, int n){

    // kód
    double result = 1; // eredmény
    for(int i = 0; i < n; i++)
        result = result * base;

    return result; // a függvény eredménye, a visszatérési érték
}

Először vizsgáljuk meg az első sort. A double a visszatérési érték típusa, vagyis megmondja, hogy mit várunk a hatványozástól (egy valós számot várunk).

Nem minden esetben van visszatérési érték, ilyenkor ide void-ot írunk

Utána a függvény neve, hatvanyozas. Ezzel tudjuk később meghívni a függvényt.

Utána a zárójelekben vesszővel elválasztva fel vannak sorolva a paraméterek(bemenetek). Az eredeti kódban ezek konkrét számok voltak, amiket a base és az n változókban tároltunk.

Végül a {  } -ek közötti code block-ban található a kód, ami minden függvényhívásban lefut, majd a végén az eredmény a return sorba kerül visszaadásra.

Vegyük észre, hogy a függvénybe nem adtuk meg a konkrét értékeket, amit ki akarunk számolni, csak egy eljárást, hogy a base és n paraméterekből hogyan kapjuk meg az eredményt.

Most úgy tudjuk kiszámolni a $latex 2^3$-at, hogy meghívjuk a hatvanyozas nevű függvényünket:

double eredmeny = hatvanyozas(2, 3);

Ilyenkor a program “átugrik” a függvényünk elejére és sorban átadja a függvénynek a megadott paramétereket. Tehát a (2, 3)-at a (base, n)-nek. Majd a függvént végén (vagy a return hívásakor) a program visszaugrik a hívás helyére és visszatér a return-ba írt értékkel.

A futtatás után ha kiiratjuk az eredmeny változó értékét megkapjuk a 8-at. Próbálkozzunk a bemeneti értékek módosításával (2, 3) és figyeljük az eredményt.

Nézzük a teljes kódot:

/**
* Hatványozó függvény
*
* @param base - hatványalap
* @param n - hatványkitevő
* @return base ^ n = base * base … * base
*/
static double hatvany(double base, int n) {
    double res = 1;

    for (int i = 0; i < n; i++)
        res = res * base;

    return res;
}

// a main függvényben:
  
double eredmeny = hatvanyozas(2, 3);
  
System.out.println(eredmeny);
  

Rekurzió

Azt nevezzük rekurziónak, ha egy függvény meghívja önmagát. Erre az órán a faktoriáis példát vettük, a következő animáció a nagyon jól elmagyarázza a működését.

A Fibonacci sorozat tagjai is így számolhatók (a kód Pythonbanvan írva, a feladat, hogy írjátok át Java-ba 🙂 )

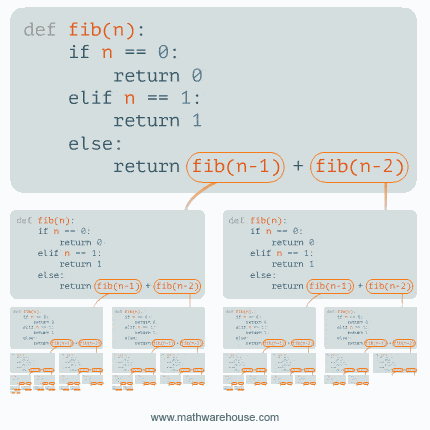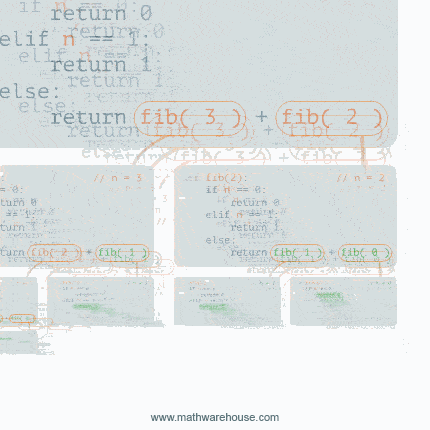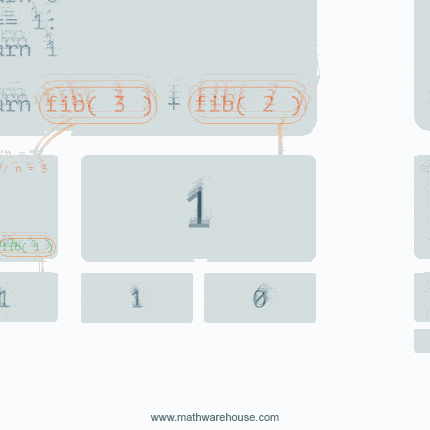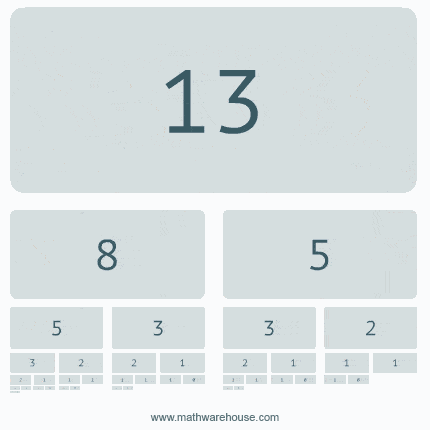
A következő órán a Class-okat (ossztály) fogjuk venni, ami az Objektum Orientált Programozás (OOP) alapja. Addig is mindenkinek jó szünetet kívánok!