Liquid Blobs with Voxelized Marching Cubes in Minecraft

Nowadays every good tech/magic mod needs a form of liquid storage. As a result they look and behave very similarly. Our mod (Crafting Pillars) is visually driven, hence I wanted to re-invent the way a Liquid Tank looks in-game while retaining the same functionality.
The Idea
Inspiration came from Portal 2 which I was playing at the time. The gels floating in the air form blobs which connect and get separated as they move relative to each other. This fitted the theme perfectly: an ancient, science fiction mod, building from stone but with technology that can compress even liquids.
To fit this into the world of Minecraft however, I had to make some changes. Minecraft is made up of Cubes and round objects are usually not welcomed.
Theory
These liquid blobs are called
metaballs and I will explain how they work.
We usually use an analogy from physics so that’s what I’m going to do. (Don’t worry, learn physics instead😉)
Imagine placing electrical charges into space. They will be at the center of our blobs. Now we have to compute the electric field strength at every point in our space.
To get the surface of the metaballs, we must choose a threshold value. We want our surface to contain every point in space where the field strength is equal to our threshold. (this is called an isosurface).
Mathematically speaking
\[\sum_{i=0}^{m} metaball_{i}(x, y, z) \leq threshold\]where m is the number of charges/blobs, \(metaball_{i}(x, y, z)\) computes the strength of the i-th charge at the location \((x, y, z)\) and threshold is an arbitrary value we choose.
The strength of a charge is inversely proportional to the square of the distance. In other words it decreases as we move further away. (\(metaball_{i}(x, y, z)=\frac{1}{(x-x_{i})^2+(y-y_{i})^2+(z-z_{i})^2}\) where \((x_{i}, y_{i}, z_{i})\) is the position of the i-th charge)
Hint: It might be interesting to play around with this function and see how the surface changes. Also try out a few different threshold values and see what works best.
Notice, that as the charges get closer together they start to connect and then completely merge as shown in image [1].
Marching Cubes Algorithm
Now that we have the equation for our surface we have to somehow display it.
In computer graphics we usually don’t render every point of a surface, but rather approximate it with triangles. Furthermore we don’t render the inside of objects, only the surface.
We divide our space into cubes along a grid and only calculate the field strengths at the grid points. We then search for the surface the following way.
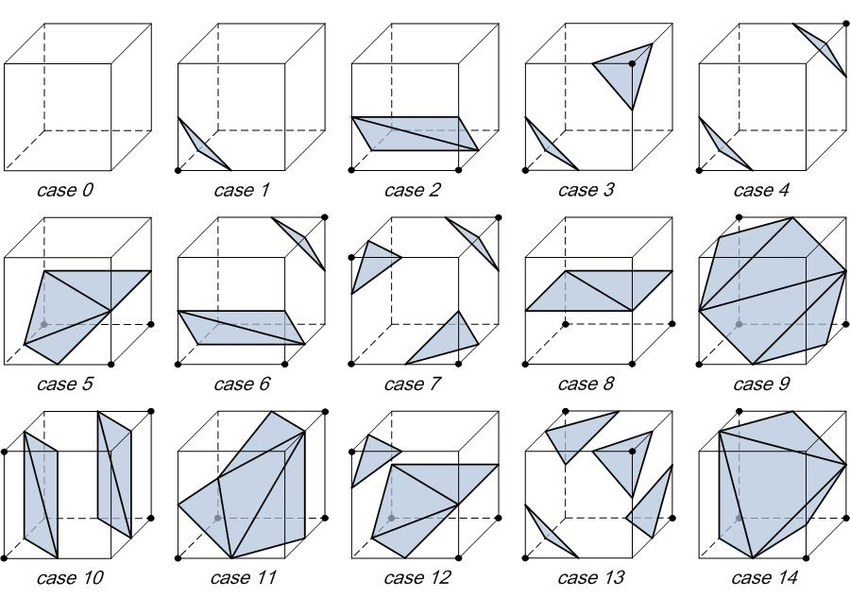
For each grid cell we check if the surface is going through it. The idea is to check the corner vertices whether they are on the opposite side of the surface. For example if one vertex is inside the surface and an adjacent vertex is outside, we know that the surface must cut the edge between these two vertices so we put some triangles there.
The original algorithm is using a look up table for each way the surface can intersect with our grid cell.
Our case is much simpler though so I won’t go into more details. There is a very good explanation here with visual illustrations.
Voxelized Algorithm
We want the surface to always align to the grid (Axis Aligned), making a nice minecraft-y look.
I created a Blobs class to store the location, strength and velocity of the charges and functions to calculate the field strength.
public static float[][][] fieldStrength(List blobs)
{
float result[][][] = new float[16][16][16];
for(int x = 0; x < 16; x++)
{
for(int y = 0; y < 16; y++)
{
for(int z = 0; z < 16; z++)
{
for(int i = 0; i < blobs.size(); i++)
{
float xDist = blobs.get(i).x - x;
float yDist = blobs.get(i).y - y;
float zDist = blobs.get(i).z - z;
float r = xDist*xDist + yDist*yDist + zDist*zDist; //distance square
result[x][y][z] += metaball(r);
}
}
}
}
return result;
}
This functions computes the field strength in a 16 * 16 * 16 grid according to the equation.
Next comes rendering.
First we iterate through each grid point and check if it is inside a blob. If it is we may have to render the side of the blob. Imagine being at the centre of the blob, the neighbouring cells are still inside so we don’t need sides there. If we need to render a side we simply render a quad from 2 triangles.
Here is the simplified code from the TileEntityRenderer:
Tessellator tess = Tessellator.getInstance();
VertexBuffer buffer = tess.getBuffer();
buffer.setTranslation(x, y, z);
buffer.begin(GL11.GL_QUADS, DefaultVertexFormats.POSITION_TEX);
final float THRESHOLD = 1;
float[][][] field = Blobs.fieldStrength(te.getBlobs());
for (int i = 0; i < 16; i++)
for (int j = 0; j < 16; j++)
for (int k = 0; k < 16; k++) if (field[i][j][k] >= THRESHOLD) { // Cell is in the blob
if (j == 15 || field[i][j + 1][k] < THRESHOLD) { // neighbour is outside (or at space bound)
buffer.pos((i) / 16F, (j + 1) / 16F, (k) / 16F).endVertex();
buffer.pos((i) / 16F, (j + 1) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j + 1) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j + 1) / 16F, (k) / 16F).endVertex();
}
if (j == 0 || (int) field[i][j - 1][k] < THRESHOLD) {
buffer.pos((i) / 16F, (j) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i) / 16F, (j) / 16F, (k) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j) / 16F, (k) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j) / 16F, (k + 1) / 16F).endVertex();
}
if (k == 15 || (int) field[i][j][k + 1] < THRESHOLD) {
buffer.pos((i) / 16F, (j + 1) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i) / 16F, (j) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j + 1) / 16F, (k + 1) / 16F).endVertex();
}
if (k == 0 || (int) field[i][j][k - 1] < THRESHOLD) {
buffer.pos((i + 1) / 16F, (j + 1) / 16F, (k) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j) / 16F, (k) / 16F).endVertex();
buffer.pos((i) / 16F, (j) / 16F, (k) / 16F).endVertex();
buffer.pos((i) / 16F, (j + 1) / 16F, (k) / 16F).endVertex();
}
if (i == 15 || (int) field[i + 1][j][k] < THRESHOLD) {
buffer.pos((i + 1) / 16F, (j + 1) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j) / 16F, (k) / 16F).endVertex();
buffer.pos((i + 1) / 16F, (j + 1) / 16F, (k) / 16F).endVertex();
}
if (i == 0 || (int) field[i - 1][j][k] < THRESHOLD) {
buffer.pos((i) / 16F, (j) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i) / 16F, (j + 1) / 16F, (k + 1) / 16F).endVertex();
buffer.pos((i) / 16F, (j + 1) / 16F, (k) / 16F).endVertex();
buffer.pos((i) / 16F, (j) / 16F, (k) / 16F).endVertex();
}
}
tess.draw();
buffer.setTranslation(0, 0, 0);
Animation
As a last step we need to animate the blobs. I store a list of blobs in the TileEntity class of the Tank.
In every tick/update I call the update function in the Blobs class for every charge:
public void update(float speed)
{
if(this.x > maxX || this.x < minX)
this.velX *= -1F;
if(this.y > maxY || this.y < minY)
this.velY *= -1F;
if(this.z > maxZ || this.z < minZ)
this.velZ *= -1F;
this.x += speed * this.velX;
this.y += speed * this.velY;
this.z += speed * this.velZ;
}
This checks if a charge (centre of a blob) is colliding with the sides of our space. We will simulate perfectly elastic collisions, so we just need to multiply the respective velocity coordinate with -1.
After that we update the position of the charge with its speed.
Final Words
That’s it, you’ve made it through!
I hope you found this useful and learnt something.